|
It
wasn't until after the discovery of non-Euclidean geometry that mathematicians began examining the foundations of Euclidean
geometry and formulating precise sets of axioms for it. The problem was to erect the entire structure of Euclidean geometry
upon the simplest foundation possible; i.e. to choose a minimum number of undefined elements and relations and a set of axioms
concerning them, with the property that all of the Euclidean geometry can be logically deduced form these without further
appeal to intuition. Hilbert's approach does address Euclid's lack of attention to the notion of undefined terms and the concepts
of incidence, betweenness and congruence. An example of Hilbert's precision and detail was to distinguish between a line and
a line segment, as Euclid did not. This topic details Hilbert's undefined terms and preliminary definitions which can be used
to provide the basis for traditional Euclidean geometry. A famous quote from Hilbert: "One must be able to say at all times-instead
of points, lines, and planes---tables, chairs, and beer mugs."
A mutual understanding of the following terms is assumed: point, line, lie on, between, congruent, set, element of, intersection,
and union. For example, two lines intersect means there is one point that lies on both of them; or said differently, two lines
are incident (have a point in common).
In geometry, definitions
are formed using known words or terms to describe a new word. There are three words in geometry that are not formally defined.
These three undefined terms are point, line and plane.
POINT
(an undefined term)
In geometry, a point has no dimension (actual
size). Even though we represent a point with a dot, the point has no length, width, or thickness. A point is usually named
with a capital letter. In the coordinate plane, a point is named by an ordered pair, (x,y).
It has no dimensions; a point
has no "size" it only designates location...
Collinear Points are points
that lie on the same line.
Coplanar Point are points that lie on the
same plane.

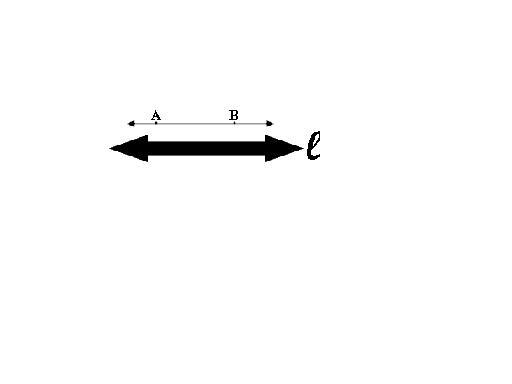
LINE (an undefined term)
In geometry, a line has no thickness but its length extends
in one dimension and goes on forever in both directions. A line is depicted to be a straight line with two arrowheads indicating
that the line extends without end in two directions. A line is named by a single lowercase letter, , or by two points on the
line, .
A line has one dimesion; a line has length (infinite) but
no width or "thickness".
Opposite rays are two rays that lie on
the same line, with common endpoint and no other points in common. Opposite rays form a straight line and/or a straight angle
(1800).
Parallel lines are two coplanar lines that do not intersect.
Skew lines are two non-coplanar lines that do not intersect.
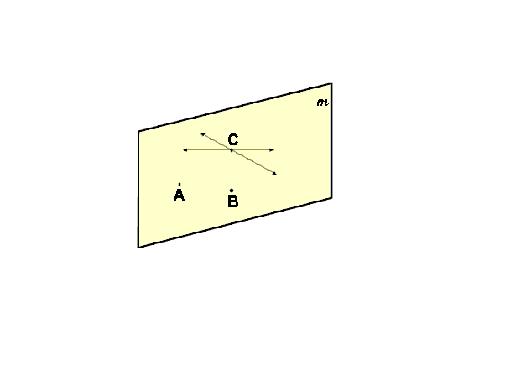
PLANE (an undefined term)
In geometry, a plane has no thickness but extends indefinitely in all directions. Planes are usually represented by a shape
that looks like a tabletop or wall. Even though the diagram of a plane has edges, you must remember that the plane has no
boundaries. A plane is named by a single letter (plane m) or by three non-collinear points (plane ABC).
|
