|
Parts of Circles
Definitions
Centre
It is in the centre
of the circle and the distance from this point to any other point on the circumference is the same.
Radius
The distance from
the centre to any point on the circle is called the radius. A diameter is twice the distance of a radius.
Circumference
The distance around
a circle is its circumference. It is also the perimeter of the circle
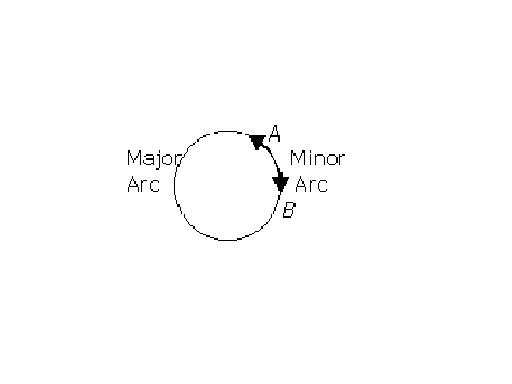
Arc
An arc is a part
of the circumference of a circle. The longer arc is called the major arc while the shorter one is called the minor arc.
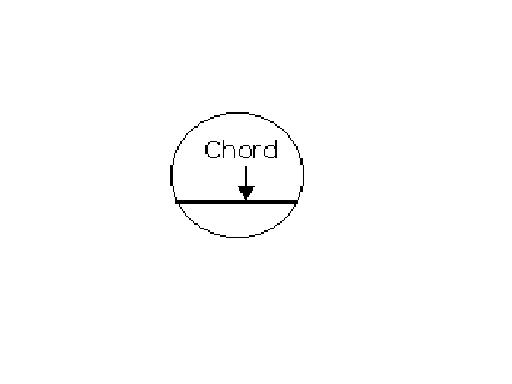
Chord
A chord is a straight line joining two points
on the circumference. The longest chord in a called a diameter. The diameter passed through the centre.
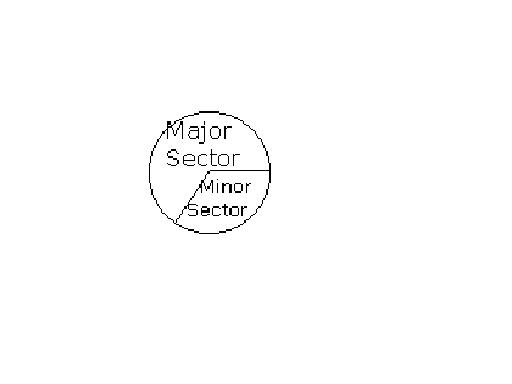
Sector
A sector is a region
enclosed by two radii and an arc. Refer to the figure given, ROS is called the angle subtened by the arc RS at the
centre O. The larger sector is called the major sector while the smaller one, a minor sector.

Segment
A segment of a circle
is the region enclosed by a chord and an arc of the circle. The larger segment is the major segment while the smaller one,
the minor segment.
Secant
A secant is a straight
line cutting at two distinct point.
Tangent
If a straight line
and a circle have only one point of contact, then that line is called a tangent. A tangent is always perpendicular to the
to the radius drawn to the point of contact. This property is abbreviated as tan ^ rad.
Although all circles are similar, note that circles are congruent if and only
if they have the same radius. We extend this concept to arcs and chords in congruent circles being congruent if and
only if they have the same measure. Several additional properties are summaried in the following theorem about chords and
the circle's center. It can be proved using the properties of the altitude, median, and perpendicular bisector of an isosceles
triangle.
|
1. The perpendicular bisector of a chord of a circle contains the center of the circle.
2. The line containing the center of a circle and perpendicular to a chord bisects the chord.
3. The bisector of the central angle of a chord perpendicularly bisects the chord.
4. The line containing the circle's center and the midpoint of a chord bisects the chord's central angle. |
Here the relationship between the measure of an inscribed angle and corresponding central angle.
|
An inscribed angle is half the measure of the central angle intercepting the same arc.
|
Since a semicircle is 180° the following is also true.
|
An angle inscribed in a semicircle is right. |
Of course,
|
If two inscribed angles intercept the same arc, then they have the same measure.
|
If you know the measure of a central angle (and radius), you can calculate the arc length of its corresponding arc
as the proportion between this measure over 360° equal to this unknown arc length over the circumference.
Example: Suppose you have a 60° arc in a circle with radius 6 m. Find its arc length A.
Solution: 60° is 1/6 of a circle, so the arc length is 1/6 the circumference: C=12 or A=2 .
A normal lens has a picture angle of about 62°, whereas a wide angle lens may be as large as 118°,
and a telephoto lens might be as small as 18°. It continues by using an inscribed angle to relate picture angle,
and in the next section, the corresponding central angle and trigonometry to find the minimal distance from the building.
Example: A camera has a 56° picture angle. Where can a person stand so that the front of a 60' building
just fills the picture.
Solution: Let the ends of the front of the building be points A and B. These form a chord of a circle O. All points
P which form a 56° inscribed angle (and are in front of the building) are places the person could stand. The corresponding
central angle would be 112°. If the person stands directly in front of the building an isosceles triangle is formed
which we can bisect and have a 28°–62°–right triangle. 30/d=tan 28° or d=30/tan
28°=56.4'.
One can construct the center of the circle by locating the point of intersection of the bisectors of two chords of
the circle (perpendicular bisector method). Using right angles and the corresponding semicircles is another way (right angle
method). Although draftsmen (and draftswomen) often use a T-square or square (ell), for drawing purposes, the corner of a
book or index card will suffice. Be able to construct or draw the center of a circle when only given an arc.
A secant is the line containing a chord. It thus intersects a circle
at the chord's two endpoints.
The measure of an angle formed by two intersecting chords
is one-half the sum of the measures of the arcs intercepted by it and its vertical angles.
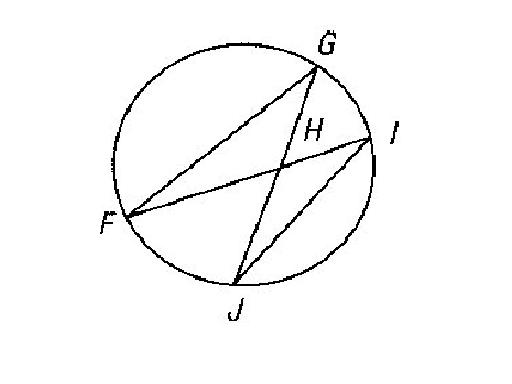
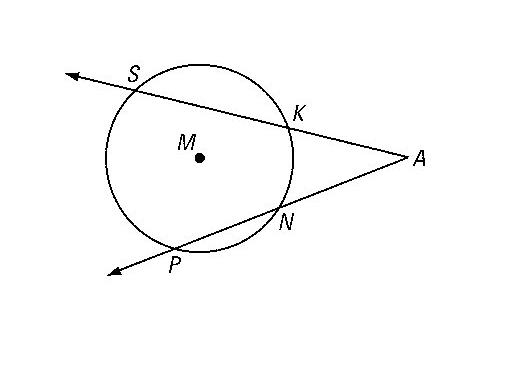
The measure of an angle formed by two secants intersecting
outside a circle is half the difference of the arcs intercepted by the angle.
|
A tangent (to a circle) is a line in the plane of the circle
which intersecting the circle at one and only one point. |
The point of tangency is the point where the line and circle intersect.
The word tangent is also used to describe other situations where circle or spheres intersect (internally tangent, externally
tangent, etc). A common tangent is a single line which is tangent to more than one object.
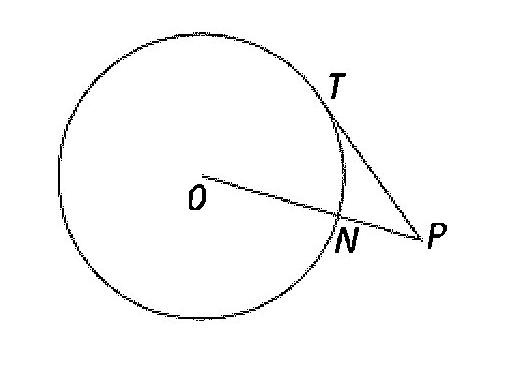
A line is perpendicular to the radius at the radius endpoint on a circle if and only if it is a tangent line.
Example:
A common application of this last theorem is to find the distance to the horizon from the top of a building, tower, or plane.
Using the value 1260', which could apply to any of these, find the desired result.
Solution: Assume the earth is a perfect sphere with r=3960 miles.
1260'=¼ miles or 0.25 miles. Using the Pythagorean theorem with the right angle at the horizon, we find the missing side is
(3960.252-39602)=44.50 miles!
The measure of an angle
formed by a tangent and a chord is half the measure of its intercepted arc.
The measure of the angle between two tangents (or between a tangent
and a secant) is the difference of the intercepted arcs.
LENGTHS OF CHORDS, SECANTS, AND TANGENTS
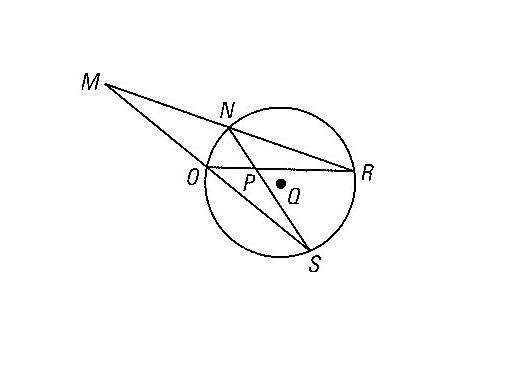
Let one secant intersect a circle at A and B and another secant intersect the circle at C and D.
If the point of intersection is P, then AP•BP=CP•DP.
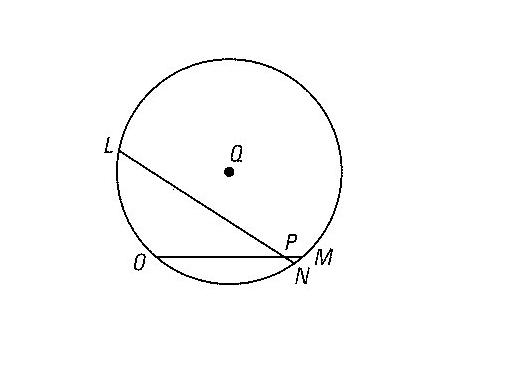
The power of point P for a circle is the square of the length
of a segment tangent to the circle from P.
Euclid's proof works whether P is inside or outside the circle! Steiner called the product used above the power of
the point P for the circle.
|
