|
|

|
|
I have
exactly four sides.
|
KINDS OF QUADRILATERALS
|

|
I have
only one set of parallel sides.
[The median of a trapezoid is parallel to the bases and equal to one-half
the sum of the bases.]
|
|
|
I have:
-
only one set of parallel sides
- base angles congruent
- legs congruent
- diagonals congruent
- opposite angles
supplementary
|
|

|
I have:
-
2 sets of parallel sides
- 2 sets of congruent sides
- opposite angles congruent
- consecutive angles supplementary
-
diagonals bisect each other
- diagonals form 2 congruent triangles
|
|
|
I have
all of the properties of the parallelogram PLUS
- 4 right angles
- diagonals congruent
|
|

|
I have
all of the properties of the parallelogram PLUS
- 4 congruent sides
- diagonals bisect angles
- diagonals perpendicular
|
|
|
Hey, look
at me!
I have all of the properties of the parallelogram AND the rectangle AND the rhombus.
I have it all!
|
TRAPEZOID
Trapezoid
is a quadrilateral that has 2 and only 2 sides parallel.
An
Isosceles Trapezoid is a trapezoid in which the nonparallel sides are congruent.
- The
base angles are congruent.
- The
diagonals are congruent
|
|
|
|
One of
the parallel sides. Every trapezoid has two bases.
|
|
|
The non-parallel
sides are legs. Every trapezoid has two legs.
|
|
|
The altitude of a trapezoid is the perpendicular distance from one base to the other. (One base may need to be extended).
|
|
|
The median
of a trapezoid is a line joining the midpoints of the two legs.
|
|
|
The usual
way to calculate the area is the average base length times altitude. See Area of a Trapezoid
|
|
Perimeter
|
The distance
a round the trapezoid. The sum of its side lengths.
|
If both legs are
the same length, this is called an isosceles trapezoid, and both base angles are the same.
If the legs are parallel,
it now has two pairs of parallel sides, and is a parallelogram.
Definition notes
There is considerable confusion over the definition
of 'trapezoid' and 'trapezium' due to differences in the British and US versions. As you can see from the table below, the
meanings of the two words are exactly reversed between the US and British interpretations.
|
Date
|
|
|
|
|
A quadrilateral with no sides parallel.
|
A quadrilateral with one pair of parallel sides.
|
|
|
A quadrilateral with one pair of parallel sides.
|
A quadrilateral with no sides parallel.
|
PARALLELOGRAM
Definition
of a Parallelogram
A parallelogram is a quadrilateral that has two pairs of parallel sides.
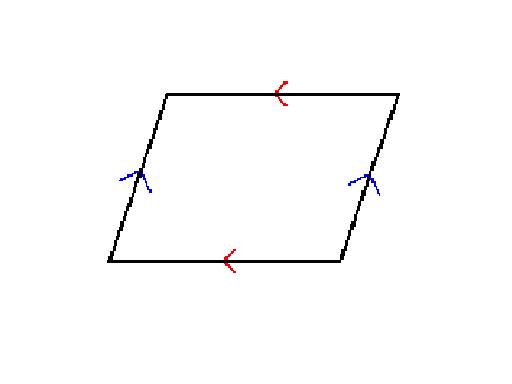
PROPERTIES OF PARALLELOGRAM
|
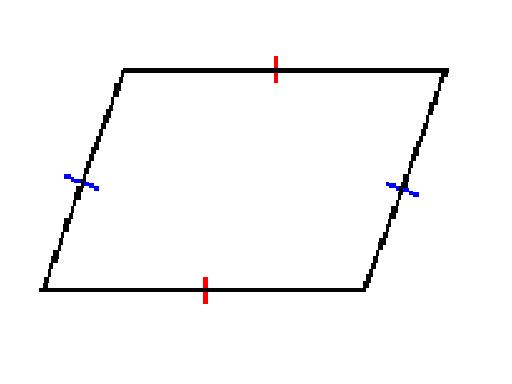
|
1. The
opposite sides are equal in length.
|
|
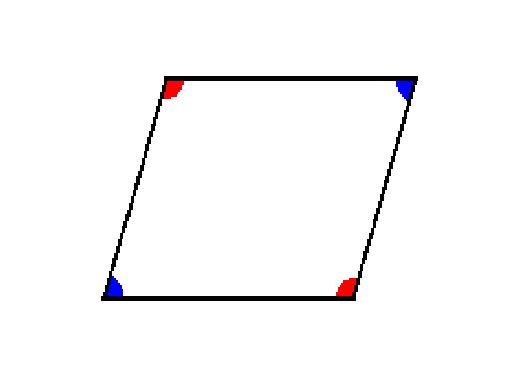
|
2. The
opposite angles are congruent.
|
|
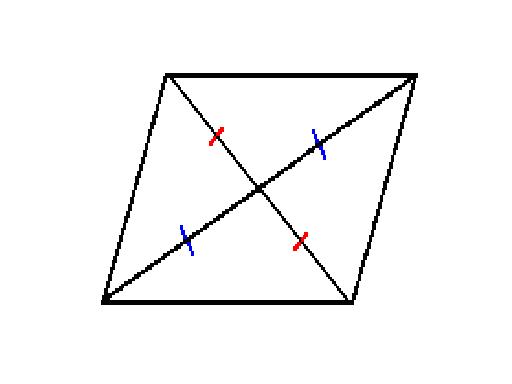
|
3. The diagonals bisect each other.
|
Conditions to be a Parallelogram
If a quadrilateral has one of the following conditions, then
it is a parallelogram.
1. If a quadrilateral has two pairs of parallel sides, then
it is a parallelogram.
2. If a quadrilateral has two pairs of opposite sides of
the same lengths, then it is a parallelogram.
3. If two pairs of opposite angles of a quadrilateral are
the same, then the figure is a parallelogram.
4. If the diagonal of a quadrilateral bisect each other,
the figure is a parallelogram.
5. If a quadrilateral has one pair of opposite sides which
are parallel and equal in length, then the figure is a parallelogram.
SPECIAL PARALLELOGRAM
RECTANGLE
The rectangle, like the
square, is one of the most commonly known quadrilaterals. It is defined as having opposite sides parallel and its corner
angles all right angles (90°) From this it follows that the opposite sides will always be the same length. Adjust the rectangle
above and satisfy yourself that this is so.
Since it is also a specific
case of a parallelogram , like a parallelogram, its diagonals bisect each other. In a rectangle the diagonals are the same length.
A rectangle can
be classified in more than one way, for example a square is a special case of a rectangle. It is also a special case of a
parallelogram (but where the angles are fixed at 90°)
RHOMBUS
Properties of a rhombus
|
|
Any side
can be considered a base. Choose any one you like. If used to calculate the area (see below) the corresponding altitude must
be used. In the figure above one of the four possible bases has been chosen.
|
|
|
The altitude of a rhombus is the perpendicular distance from the base to the opposite side (which may have to be extended).
In the figure above, the altitude corresponding to the base CD is shown.
|
|
|
There are
several ways to find the area of a rhombus. The most common is (base × altitude). Each is described in Area of a rhombus
|
|
|
|
The Diagonals of a Rhombus
The diagonals of a rhombus always bisect each other at 90°. Some find this surprising and not at all obvious. Reshape the
rhombus above and convince yourself that the diagonals always cross at right angles.
SQUARE
The square is probably the best known of the quadrilaterals. It is defined as having all sides equal, and its interior angles
all right angles (90°). From this it follows that the opposite sides are also parallel.
A square is simply a specific case of a regular polygon, in this case with 4 sides. All the facts and properties described
for regular polygons apply to a square. See Regular Polygons
|
|
|
|
The vertex (plural: vertices) is a corner of the square. Every square has four
vertices.
|
|
|
The distance around the square. All four sides are by definition the same
length, so the perimeter is four times the length of one side, or:
perimeter = 4s where s is the length of one side. See
also Perimeter of a square.
|
|
Area
|
Like most quadrilaterals, the area is the length of one side times the
perpendicular height. So in a square this is simply:
area = s2
where s is the length of one side. See
also Area of a square.
|
|
|
Each diagonal of a square is the perpendicular
bisector of the other. That is, each cuts the other into two equal parts, and they cross
and right angles (90°).
The length of each diagonal is s√2 where sis the length of any one side.
|
A square can be thought of as a special case of other quadrilaterals, for example
KITE
A kite is a member of the quadrilateral family, and while easy to understand visually, is a little tricky to
define in precise mathematical terms. It has two pairs of equal sides. Each pair must be adjacent sides (sharing a common vertex) and each pair must be distinct. That
is, the pairs cannot have a side in common.
Drag all the orange dots
in the kite above, to develop an intuitive understanding of a kite without needing the precise 'legal' definition.
Properties of a kite
- Diagonals intersect at right angles.
In the figure above, click 'show diagonals' and reshape the
kite. As you reshape the kite, notice the diagonals always intersect each other at 90°
- Angles between unequal sides are equal
In the figure
above notice that ∠ABC = ∠ADC no matter how how you reshape the kite.
- Area
The area of a kite can be calculated in various
ways. See Area of a Kite
- Perimeter
The distance around the kite. The sum of its
sides. See Perimeter of a Kite
- A kite can become a rhombus
In the special case where all 4 sides are the same length, the kite
satisfies the definition of a rhombus. A rhombus in turn can become a square if its interior angles are 90°. Adjust the kite above and try
to create a square.
|
