|
In Plane Geometry, two objects are congruent if all of their corresponding parts are congruent. In the first diagram,
the two triangles have two sides which are congruent, and the angle between these sides is also congruent. Euclid
proved that they are congruent triangles (Theorem I.4, called "Side-Angle-Side" of SAS). But, he was not happy with the proof,
as he avoided similar proofs in other situations. The way he proved it, is to move one triangle until it is superimposed on
the other triangle. Such a trick (superposition: placing one triangle on top of another, to see if they are congruent), is
not considered legal, now. It involves some complicated assumptions. So, now this (SAS) is given as an assumption (postulate).
It is the Side-Angle-Side Postulate. Euclid proved his Side-Side-Side (SSS)
Theorem (I.8) and his Angle-Side-Angle (ASA, diagram at the right) Theorem (I.26) in a similar way. In SSS, if a triangle
has all three sides conguent to the corresponding sides of a second triangle, then they are congruent. In ASA, if a triangle
has two angles and the side in between the angles congruent to the corresponding parts of a second triangle, then they are
congruent. These too, are now assumed as postulates. It is easy to construct
a triangle given the lengths of the three sides (diagram on the left), or two sides and the included angle, or two angles
and the included side. Given the ease of these constructions (especially SSS), it seems strange that the corresponding congruence
"theorems" cannot be proven, except by slightly shady means (superposition). All three of these congruence postulates are equivalent. You can assume any one of them, and prove
the other two from there. Euclid also proved an Angle-Angle-Side
(AAS) as a corollary (a minor theorem derived directly from the parent theorem) to Theorem I.26. The situation SSA (or ASS) is not a theorem or postulate, as it is often ambiguous,
there are often two different non-congruent triangles with two congruent sides and a congruent angle at the end of one of
the sides.
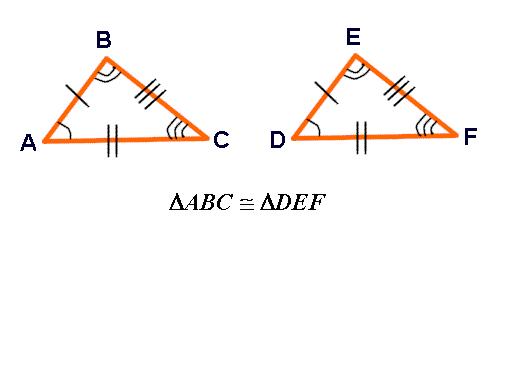
When two triangles
are congruent, there are 6 facts that are true about the triangles:
- there are 3 sets of congruent (equal) sides and
- there are 3 sets of congruent (equal) angles.
NOTE: The corresponding congruent sides are marked
with small straight line segments called hash marks. The corresponding congruent angles are marked with arcs.
The
6 facts of congruent triangles:
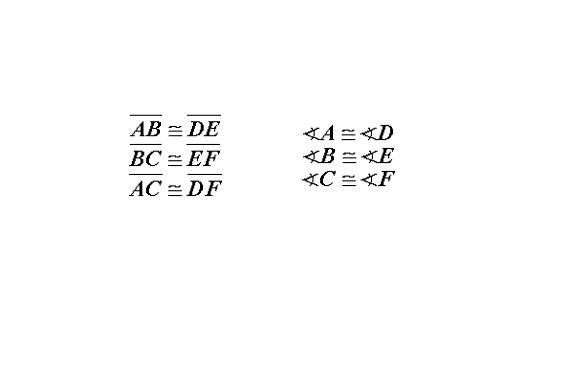
Note:
The order of the letters in the names of the triangles displays the corresponding relationships. Even without
the picture, you would know that <A would be congruent to <D, and segment BC would be congruent to segment EF, because
they are in the same position in each triangle name.
Six
facts for every set of congruent triangles! Fortunately, when we need to PROVE (or show) that triangles are congruent, we
do NOT need to show all six facts are true. There are certain combinations of the facts that are sufficient to prove
that triangles are congruent.

TWO
– COLUMN PROOF
A kind of proof in which the statements (conclusions) are listed in one column, and the reasons for each statement's truth
are listed in another column. Identical in content, but different in form, from a paragraph proof.
|
